相対論を用いてタイムトラベルを語るのは強引か？

タイムトラベルという言葉を用いるとき，ときどき半半ば強引に「相対論によると」光速に近ければ時間は遅くなるという話が存在する．確かに光速で進む物体の時間は静止系よりも時間がゆっくり進むことになるし，一種のタイムトラベルとも言えそうである．

しかし，双子のパラドックスという概念を引き合いにしてその理屈はおかしいと主張する人が少数いる．

実際どうなのか検討する記事である．

まず，結論を先に話すと双子のパラドックスの問題解消のために，一般相対論を出すものもいるが，一般相対論なんかを使わずとも特殊相対論で十分に解消できる．

さらに，光速で進む物体の時間は静止系よりも時間がゆっくり進むし，慣性系に戻ってきても時間は相対的には遅れている．つまり，同い年だったのに数年後には10歳差ということもありうる．

相対論の復習
#

光速 $c$ に近い速度で進む物体においてはNewtonの運動方程式は適応できない．このような状況では相対論的効果も考慮し，考えなくてはいけない．

今回のタイトルでは「世界距離」という言葉を使わせていただいたが，書籍によっては「世界間隔」と表記するものも多い．どちらも同じことを指しているので本サイトでは前者で統一する．

世界距離は四次元座標 $x^\mu$，Minkowski計量 $\eta_{\mu \nu}$を用いて

$$ ds^2 = \eta_{\mu \nu} dx^\mu dx^\nu $$

と表せる．ここで地球に観測者がいる系を静止系と呼び，光速で移動している系を移動系ということにする．静止系において光速で移動している観測者を見るとその移動距離は $c^2 dt^2$ であるから世界距離

$$ d s^2 = \eta_{\mu \nu} dx^\mu dx^\nu = - c^2 dt^2 + c^2 dt^2 = 0 $$

がいえる．

また，移動系においては観測者は静止しているので世界距離

$$ ds’^2 = \eta_{\mu \nu} dx’^\mu dx’^\nu = 0 - c^2 dt’^2 $$

がいえる．ただ世界距離はLorentz不変であるから

$$ ds^2 = ds’^2 $$

がいえる．ゆえに，$dt’ = 0$ がいえて時間は静止しているように見えることが分かる．

ここでどんなパラドックスが生じるかといえば以上の議論はあくまでも相対的な事柄でしか無い．

つまり，光速で移動している系（移動系）から地球を見れば地球が光速で移動しているわけである．つまり，移動系から見れば静止系の時間が止まっているし，静止系から見れば移動系の時間が止まっているのである．

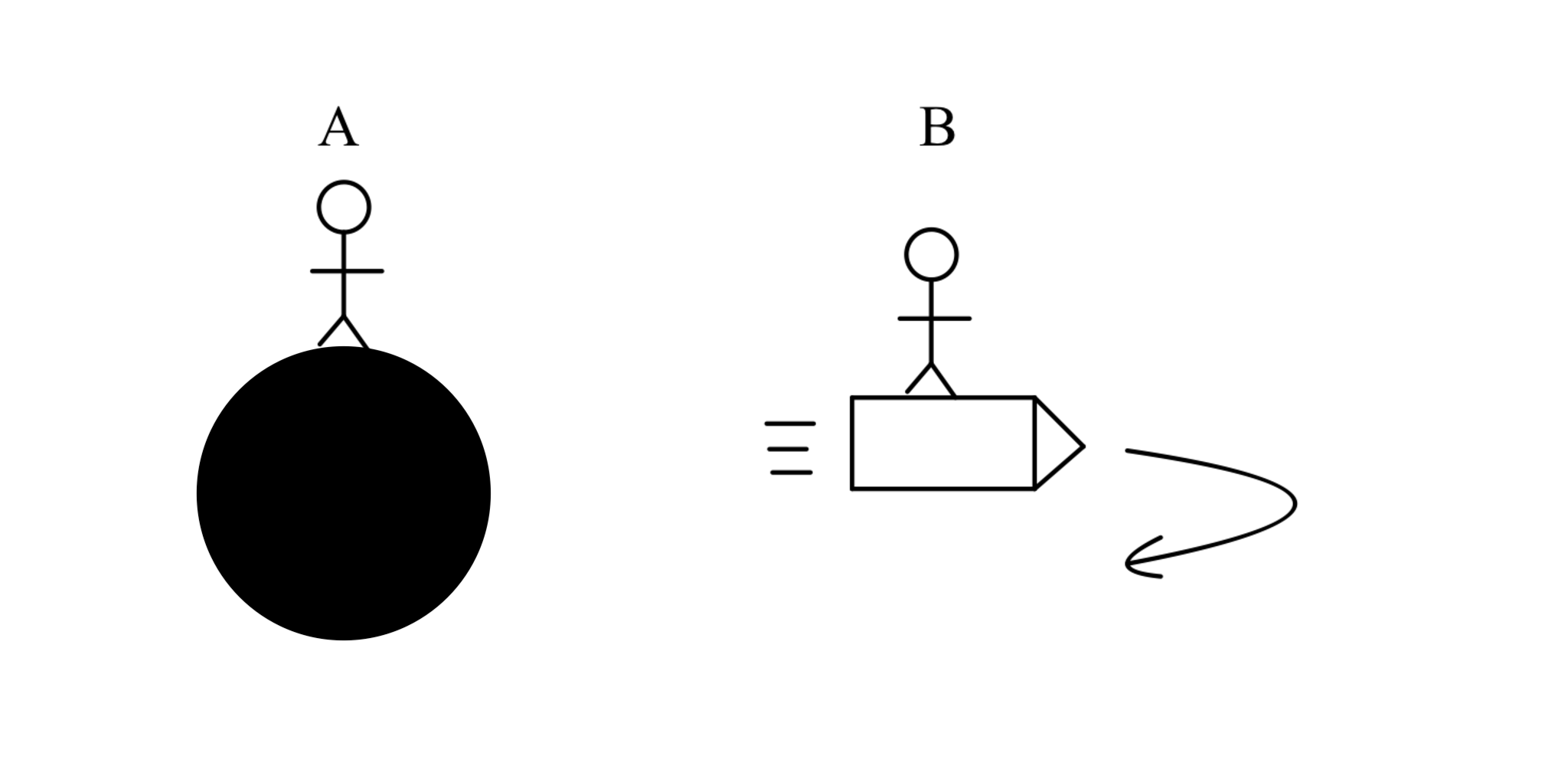
すなわち双子A, Bのうち片方Bだけが光速で地球から旅をして帰ってきたとき異なる時間を持つ（お互い相手の時計は止まってると思っている）二人が出会うため，矛盾が生じてしまう．これを双子パラドックスと呼んでいる．

これは単純な問題である．上の議論は特殊相対性原理に則っているため，慣性系でしか議論はできない．しかし，移動系は一旦，地球に戻るためにUターンもしくは減速を行うはずである．つまりこの際に慣性系は破れ加速度系となってしまう．

ゆえに，移動系から見てはいけないのだ．

地球（静止系）は常に慣性系であるのでこちらで議論した結末は問題なく正しい．ゆえに，双子の片方Bは光速で移動しているため時間は静止しているため出発時と同じ年齢で時間は一切進まずに帰ってくる，というのが正解となる．

一般相対論など不必要であるし，きちんと慣性系のみだけで議論すればいいだけの話である．

タイムトラベルというのが何なのかの定義付けにはよるが，上で議論したように実際に移動した系とそうでない系で時間に隔たりができる．

それゆえ，タイムトラベルと呼ぶのは問題ないだろうし強引とまでは言い難いのかもしれない．